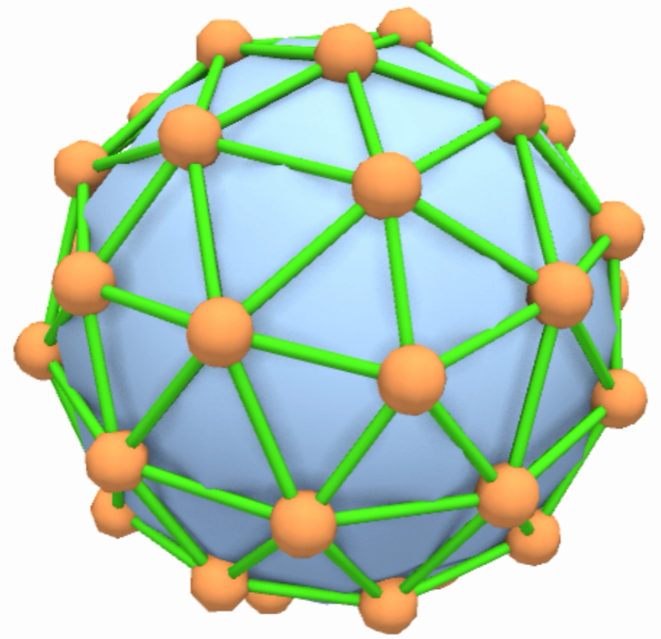
Variational Inference
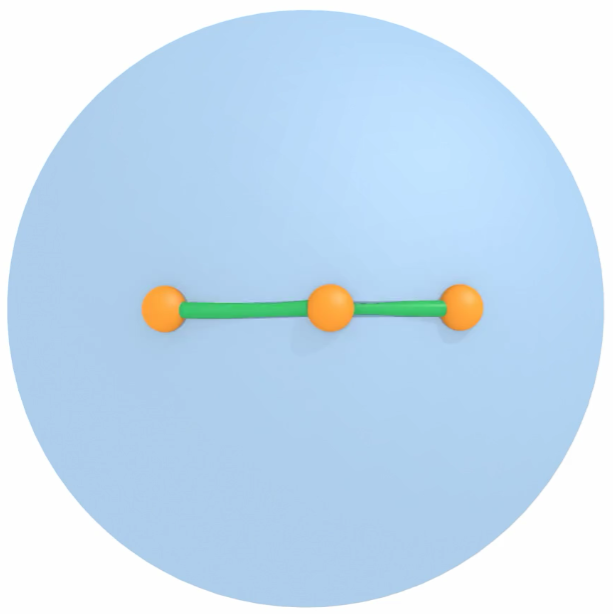
Scaling Gaussian Processes with Derivatives
Augmenting Gaussian Processes (GP) with derivative information can significantly enhance their predicitive capacity. However, there are serious scalability issues associated with training and inference when using GPs with derivatives, particularly in high dimensions. We developed a Variational Inference technique for training GPs with derivatives that learns a reduced GP model, allowing for scalable training and inference at a minimal loss in accuracy.
Bayesian Optimization
High Dimensional Bayesian Optimization with Derivative Information
Global optimization in high dimensions is hard. By leveraging Stochastic Variational Gaussian Processes that can scalably incorporate derivative information within a Bayesian optimization loop we can accelerate global optimization and efficiently find solutions.
Particle Accelerators
Derivative-Free Optimization of a Rapid-Cycling Synchrotron
Fermilab houses a proton accelerator to be used as a part of Deep Underground Neutrino Experiment (DUNE), an international, multi-decadal physics program for leading-edge neutrino science and proton decay studies. However by the inception of DUNE in 2032, the FermiLab proton complex must undergo a substantial upgrade in order to meet the particle acclerator beam power requirements. I developed and solved a derivative-free optimization model which seeks these high power accelerator configurations.

Constrained Optimization
Modeling Approaches for Addressing Simple Unrelaxable Constraints with Unconstrained Optimization Methods
When optimizing chemical concentrations in a chemical system or probabilities of transmission in an epedemiological simulation, negative concentration levels and negative probabilities, respectively, are readily modeled as belonging to regions that an optimization algorithm should never probe. These constraints are known as unrelaxable constraints, constraints which must be satisfied in order to produce meaningful output of the objective. Solving optimization problems with unrelaxable constraints is difficult, and traditionally requires specialized algorithmic solutions. We have developed modeling approaches which open the doors to "off-the-shelf" optimization routines, such as BFGS, to solve optimization problems with simple unrelaxable constraints.
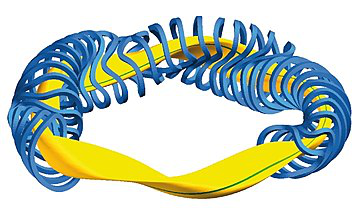
Fusion Energy
Stochastic Optimization of Stellarator Coil Designs
The Stellarator is a state-of-the-art nuclear fusion device designed to generate sustainable energy. We are developing a stochastic optimization framework within FOCUS, an optimization toolbox for designing the magnetic coils for Stellarators. Our accelerated stochastic optimization methods allow for rapid development of coils with low construction tolerances, with the goal of saving millions of dollars in engineering costs.
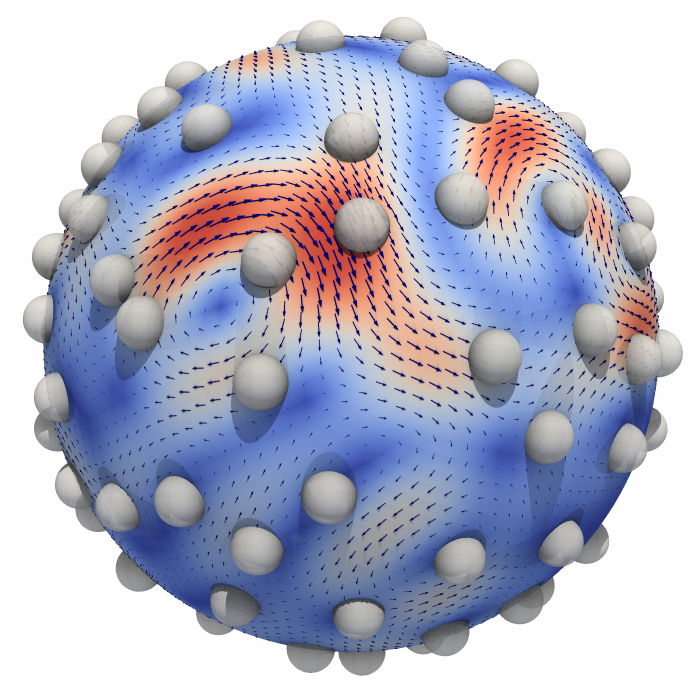
Microstructures
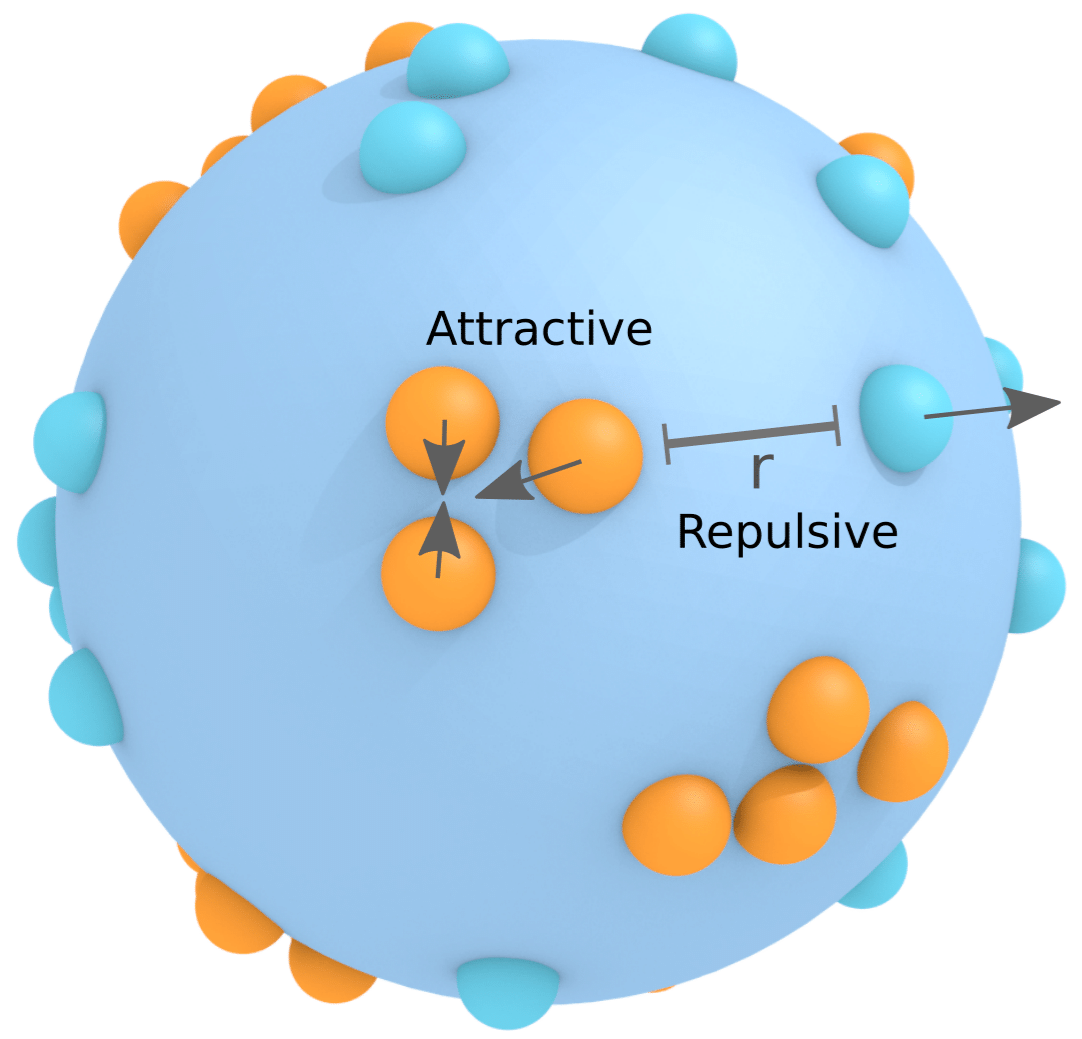
Fluctuating Hydrodynamics Methods for the Drift-Diffusion Dynamics of Microstructures
The goal of this project was to study the Drift-Diffusion Dyanamics of Microstructures embedded in spherical fluid interfaces. In nature we find that this is a good model for the interaction of proteins in the lipid-bilayer membrane (cell membrane). Throughout the project we developed fluctuating hydrodynamics approaches for capturing the fluid and microstructure interactions. We then used our model to study how the drift-diffusion dynamics of microstructures compare with and without hydrodynamic coupling within the curved fluid interface.